त्रिभुज Ex 6.3

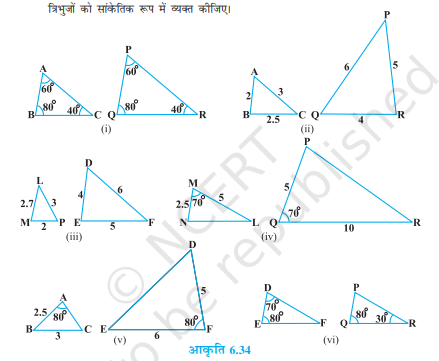
प्रश्न 1. बताइए कि आकृति में दिए त्रिभुजों के युग्मों में से कौन-कौन से युग्म समरूप हैं। उस समरूपता कसौटी को लिखिए जिसका प्रयोग आपने उत्तर देने में किया है तथा साथ ही समरूप त्रिभुजों को सांकेतिक रूप में व्यक्त कीजिए।

प्रश्न 2. आकृति में, ∆ODC ~ ∆OBA, ∠BOC = 125° और ∠CDO = 70° है। ∠DOC, ∠DCO और ∠OAB ज्ञात कीजिए।

प्रश्न 3. समलम्ब ABCD जिसमें AB || DC है, के विकर्ण AC और BD परस्पर O पर प्रतिच्छेद करते हैं। दो त्रिभुजों की समरूपता कसौटी का प्रयोग करते हुए, दर्शाइए कि OA/OC=OB/OD है।

प्रश्न 4. दी गई आकृति में, QR/QS=QT/PR तथा ∠1 = ∠2 है। दर्शाइए कि ∆PQS ~ ∆TQR है।

प्रश्न 5. ∆PQR की भुजाओं PR और QR पर क्रमशः बिन्दु S और T इस प्रकार स्थित हैं कि ∠P = ∠RTS है। दर्शाइए कि ∆RPQ ~ ∆RTS है।

प्रश्न 6. दी गई आकृति में, यदि ∆ABE ≅ ∆ACD है तो दर्शाइए कि ∆ADE ~ ∆ABC है।

प्रश्न 7. दी गई आकृति में, ∆ABC के शीर्ष लम्ब AD और CE परस्पर बिन्दु P पर प्रतिच्छेद करते हैं। दर्शाइए कि-
(i) ∆AEP ~ ∆CDP
(ii) ∆ABD ~ ∆CBE
(iii) ∆AEP ~ ∆ADB
(iv) ∆PDC ~ ∆BEC

प्रश्न 8.  समान्तर चतुर्भुज ABCD की बढ़ाई गई भुजा AD पर स्थित E एक बिन्दु है तथा BE भुजा CD को F पर प्रतिच्छेद करती है। दर्शाइए कि ∆ABE ~ ∆CFB हैं।

प्रश्न 9. दी गई आकृति में, ABC और AMPदो समकोण त्रिभुज हैं, जिनके कोण B और M समकोण हैं। सिद्ध कीजिए कि-
(i) ∆ABC ~ ∆AMP
(ii) CA/PA=BC/MP

प्रश्न 10. CD और GH क्रमशः ∠ACB और ∠EGF के ऐसे समद्विभाजक हैं कि बिन्दु D औरत क्रमशः ∆ABC और ∆FEG की भुजाओं AB और FE पर स्थित हैं। यदि ∆ABC ~ ∆FEG हो तो दर्शाइए कि-
(i) CD/GH=AC/FG
(ii) ∆DCB ~ ∆HGE
(iii) ∆DCA ~ ∆HGF

प्रश्न 11. दी गई आकृति में, AB = AC वाले, एक समद्विबाहु त्रिभुज ABC की बढ़ाई गई भुजा CB पर स्थित E एक बिन्दु है। यदि AD ⊥ BC और EF ⊥ AC है तो सिद्ध कीजिए कि ∆ABD ~ ∆ECF है।

प्रश्न 12. एक त्रिभुज ABC की भुजाएँ AB और BC तथा माध्यिका AD एक अन्य त्रिभुज PQR की क्रमशः भुजाओं PQ और QR तथा माध्यिका PM के समानुपाती हैं। दर्शाइए कि ∆ABC ~ ∆PQR है।

प्रश्न 13. किसी त्रिभुज ABC की भुजा BC पर एक बिन्दु D इस प्रकार स्थित है कि ∠ADC = ∠BAC है। दर्शाइए कि CA2 = CB . CD

प्रश्न 14. एक त्रिभुज ABC की भुजा AB और AC तथा माध्यिका AD, एक अन्य त्रिभुज PQR की भुजाओं PQ और PR तथा माध्यिका PM के समानुपाती हैं। दर्शाइए कि ∆ABC ~ ∆PQR है।

प्रश्न 16. AD और PM त्रिभुजों ABC और PQR की क्रमशः माध्यिकाएँ हैं, जबकि ∆ABC ~ ∆PQR है। सिद्ध कीजिए कि ABPQ=ADPM है।