BSEB Bihar Board Class 10 Maths Solutions Chapter 6 त्रिभुज Ex 6.2
Bihar Board Class 10 Maths त्रिभुज Ex 6.2
प्रश्न 1. आकृति में, DE || BC है। चित्र (i) में EC और चित्र (ii) में AD ज्ञात कीजिए-
प्रश्न 2. किसी ∆PQR की भुजाओं PQ और PR पर क्रमशः बिन्दु E और F स्थित हैं। निम्नलिखित में से प्रत्येक स्थिति के लिए, बताइए कि क्या EF || QR है-
(i) PE = 3.9 cm, EQ = 3 cm, PF = 3.6 cm और FR = 2.4 cm
(ii) PE = 4 cm, QE = 4.5 cm, PF = 8 cm और RF = 9 cm
(iii) PQ = 1.28 cm, PR = 2.56 cm, PE = 0.18 cm और PF = 0.36 cm
प्रश्न 3. आकृति में, यदि LM || CB और LN || CD हो तो सिद्ध कीजिए कि AM/AB=AN/AD है।
प्रश्न 4. आकृति में, DE || AC और DF || AE है। सिद्ध कीजिए कि BF/FE=BE/EC है।
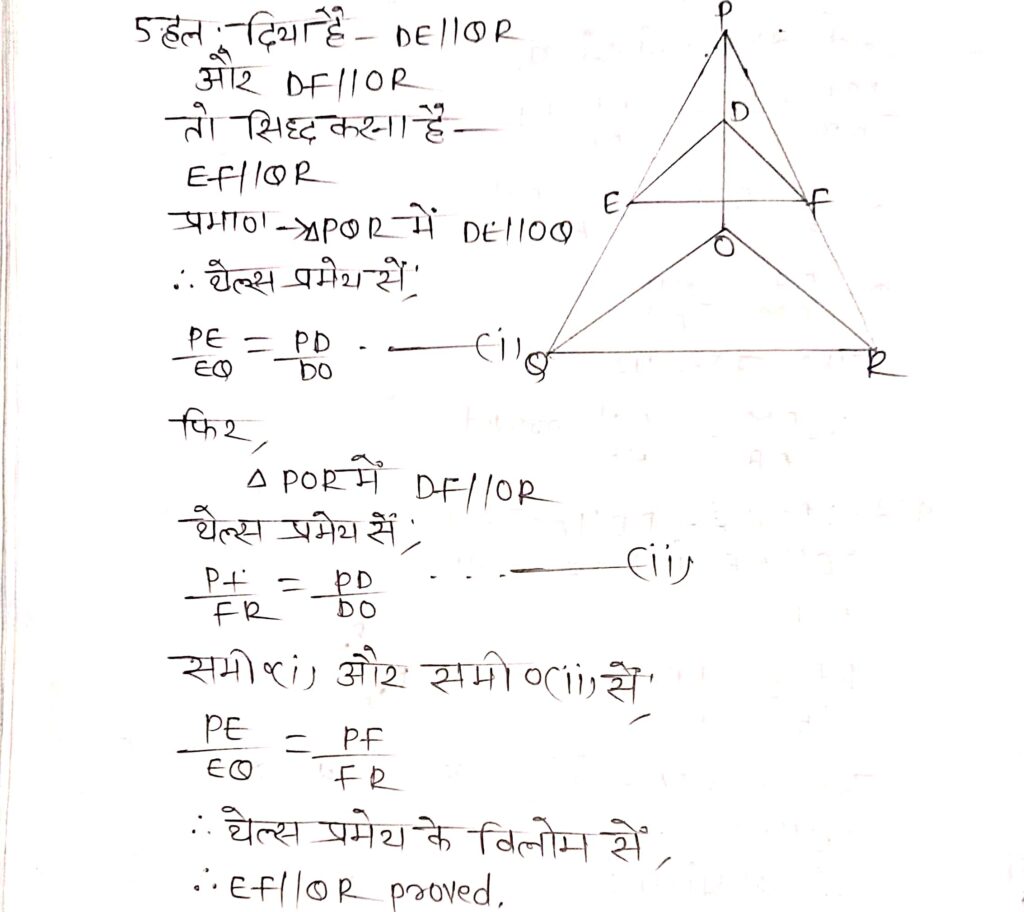
प्रश्न 5. आकृति में, DE || OQ और DF || OR है। दर्शाइए कि EF || QR है।
प्रश्न 6. आकृति में क्रमशः OP, OQ और OR पर स्थित बिन्दु A, B और C इस प्रकार हैं कि AB || PQ और AC || PR है। दर्शाइए कि BC || QR है।
प्रश्न 7. आधारभूत आनुपातिक प्रमेय का प्रयोग करते हुए सिद्ध कीजिए कि एक त्रिभुज की एक भुजा के मध्य-बिन्दु से होकर दूसरी भुजा के सामान्तर खींची गई रेखा तीसरी भुजा को समद्विभाजित करती है।
प्रश्न 8. आधारभूत आनुपातिक प्रमेय के विलोम का प्रयोग करते हुए सिद्ध कीजिए कि एक त्रिभुज की किन्हीं दो भुजाओं के मध्य-बिन्दुओं को मिलाने वाली रेखा तीसरी भुजा के समान्तर होती है।
प्रश्न 9. ABCD एक समलम्ब है जिसमें AB || DC है। इसके विकर्ण परस्पर बिन्दु O पर प्रतिच्छेद करते हैं। दर्शाइए कि AOBO=CODO है।
प्रश्न 10. एक चतुर्भुज ABCD के विकर्ण परस्पर बिन्दु पर इस प्रकार प्रतिच्छेद करते हैं कि AO/BO=CODO है। दर्शाइए कि AB/CD एक समलम्ब है।
