त्रिकोणमिति का परिचय Ex 8.2

त्रिकोणमिति का परिचय Ex 8.2
मैट्रिक परीक्षा 2023 (Matric Exam 2023) की तैयारी करना चाहते हैं तो आपको यहां पर कक्षा 10 गणित (Class 10th Mathematics Question Answer) का कक्षा 10 त्रिकोणमिति क्वेश्चन आंसर (Class 10th Trikonamiti subjective Question Answer 2023) यहां पर दिया गया है तथा अगर आप लोग क्लास 10th मैथ का मॉडल पेपर (Class 10th Model Paper) पढ़ना चाहते हैं तो आपको इस वेबसाइट पर मिल जाएगा और त्रिकोणमिति का सब्जेक्टिव प्रश्न उत्तर (Class 10th Trigonometry Subjective Question Answer 2023) पढ़ना चाहते हैं तो लिंक पर क्लिक करके इसे आप पढ़ सकते हैं।
त्रिकोणमिति का परिचय Ex 8.2
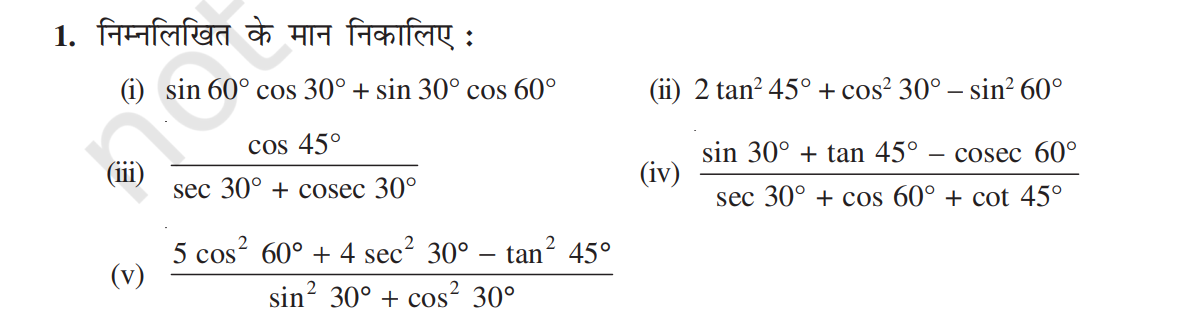
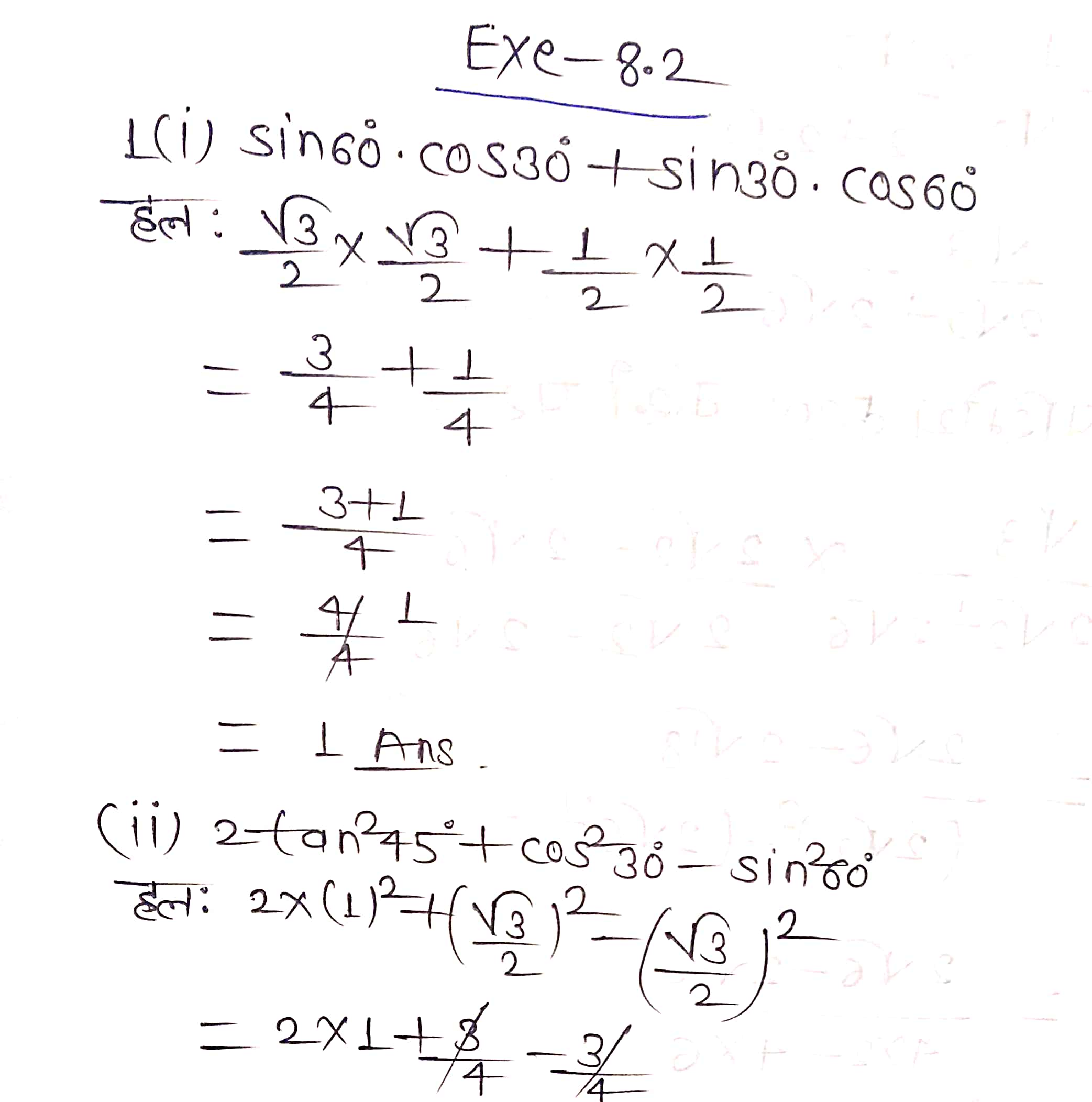

![]()
त्रिकोणमिति का परिचय Ex 8.2


![]()
त्रिकोणमिति का परिचय Ex 8.2
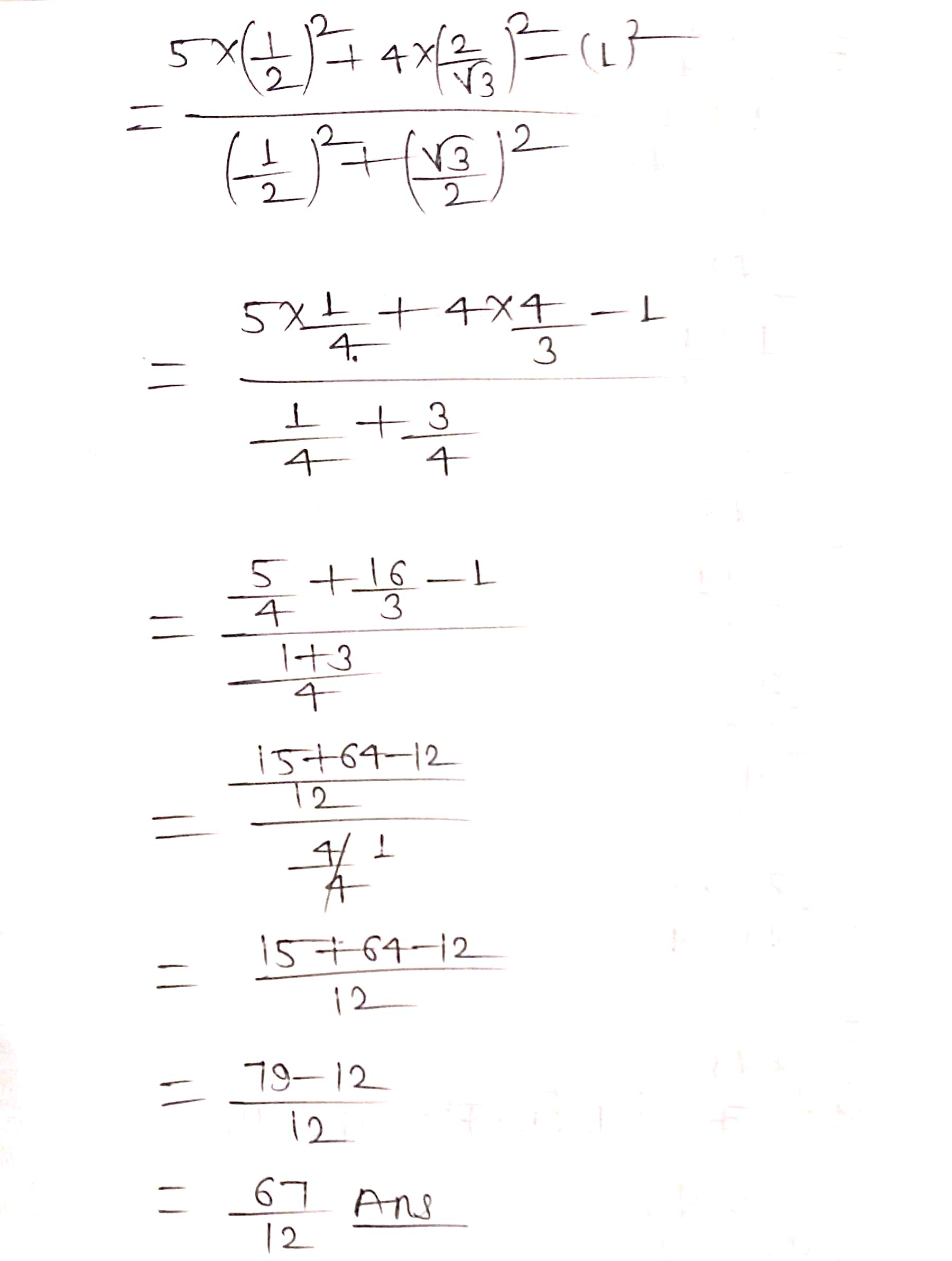
प्रश्न 2. सही विकल्प चुनिए और अपने विकल्प का औचित्य दीजिए–



त्रिकोणमिति का परिचय Ex 8.2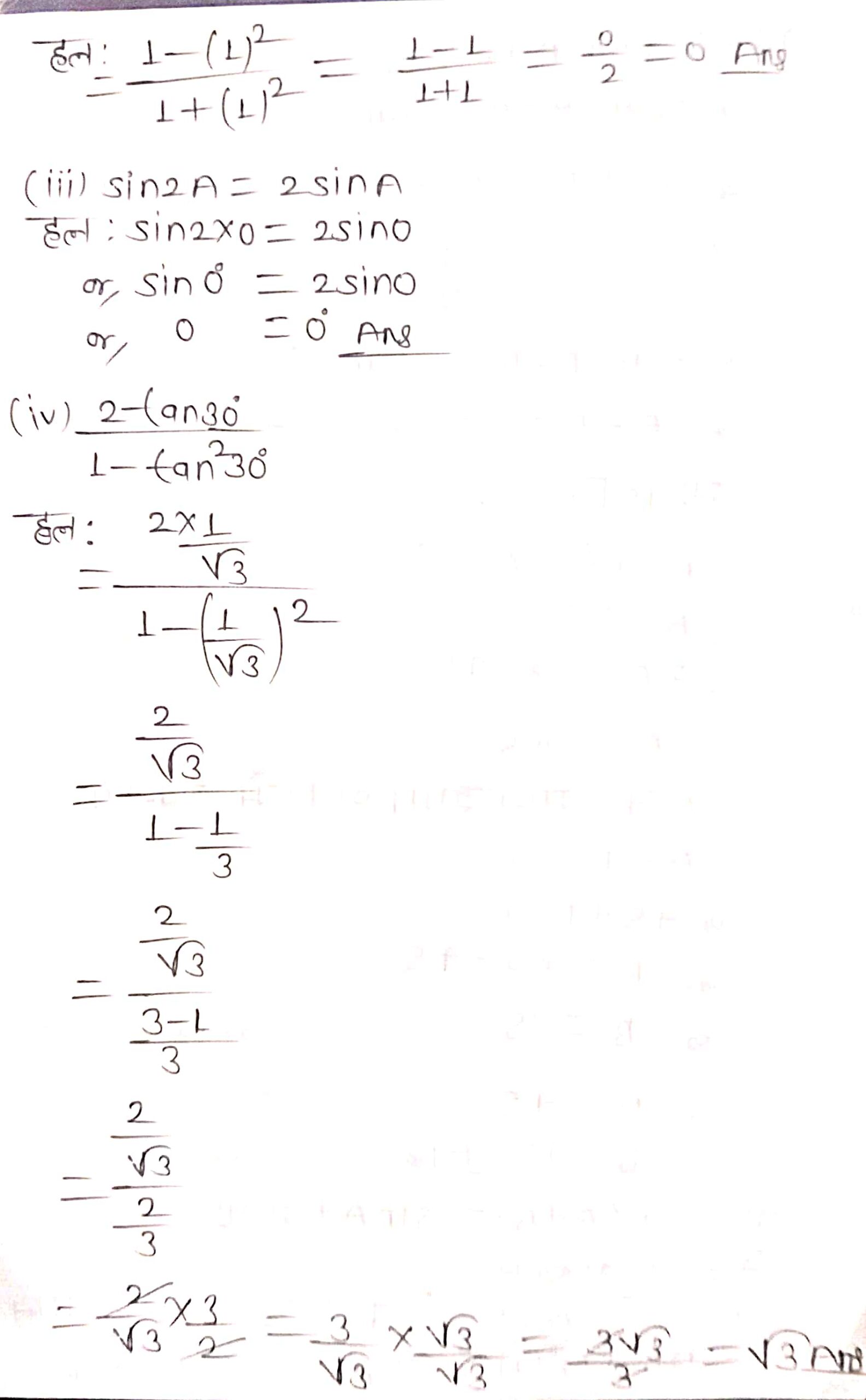
त्रिकोणमिति का परिचय Ex 8.2
प्रश्न 3. यदि tan(A + B) = √3 और tan(A – B) = 13√; 0° < A + B < 90°; A > B, तो A और B का मान ज्ञात कीजिए।

त्रिकोणमिति का परिचय Ex 8.2
प्रश्न 4. बताइए कि निम्नलिखित में कौन-कौन सत्य हैं या असत्य हैं। कारण सहित अपने उत्तर की पुष्टि कीजिए।
(i) sin(A + B) = sin A + sin B
(ii) θ में वृद्धि होने के साथ sin θ के मान में भी वृद्धि होती है।
(iii) θ में वृद्धि होने के साथ cos θ के मान में भी वृद्धि होती है।
(iv) θ के सभी मानों पर sin θ = cos θ
(v) A = 0° पर cot A परिभाषित नहीं है।



मैट्रिक परीक्षा 2023 (Matric Exam 2023) की तैयारी करना चाहते हैं तो आपको यहां पर कक्षा 10 गणित (Class 10th Mathematics Question Answer) का कक्षा 10 त्रिकोणमिति क्वेश्चन आंसर (Class 10th Trikonamiti subjective Question Answer 2023) यहां पर दिया गया है तथा अगर आप लोग क्लास 10th मैथ का मॉडल पेपर (Class 10th Model Paper) पढ़ना चाहते हैं तो आपको इस वेबसाइट पर मिल जाएगा और त्रिकोणमिति का सब्जेक्टिव प्रश्न उत्तर (Class 10th Trigonometry Subjective Question Answer 2023) पढ़ना चाहते हैं तो लिंक पर क्लिक करके इसे आप पढ़ सकते हैं।
त्रिकोणमिति क्या है?
विभिन्न कोणों (0 से 90 डिग्री) के लिए कक्षा 10 के त्रिकोणमिति और त्रिकोणमितीय अनुपातों का प्रयोग करने के बाद इसका उपयोग आर्किटेक्चर, इंजीनियरिंग, भौतिक विज्ञान जैसे सब्जेक्ट्स में देख सकते हैं। त्रिकोणमिति गणित की वह शाखा है, जिसमें त्रिभुज की तीनों भुजाओं और तीनों कोणों की स्टडी की जाती है। त्रिकोणमिति को इंग्लिश में Trigonometry कहते हैं और त्रिकोणमिति का अर्थ त्रिभुज की तीनों भुजाओं की माप होता है।
त्रिकोणमिति की खोज किसने की थी?
त्रिकोणमिति का आविष्कार और प्रयोग प्राचीन भारत में किया गया। त्रिकोणमिति के जनक, शून्य और दशमलव का महत्व बताने वाले विश्व के महान गणितज्ञ और खगोलशास्त्री आर्यभट्ट हैं।
ट्रिगोनोमेट्रिक आइडेंटिटी की इम्पोर्टेंस
ट्रिगोनोमेट्रिक आइडेंटिटी का उपयोग त्रिकोणमिति और ज्यामिति की समस्याओं को हल करने और विभिन्न गणितीय गुणों को समझने के लिए किया जाता है। प्रमुख ट्रिग आइडेंटिटी जानने से महत्वपूर्ण गणितीय सिद्धांतों को याद रखने और समझने में मदद मिलती है और इससे गणित की कई समस्याओं को हल किया जा सकता है।
त्रिकोणमिति का उपयोग
त्रिकोणमिति का उपयोग मैथ, साइंस और टेक्नोलाॅजी में किया जाता है। त्रिकोणमिति की स्टडी के बाद हम इसका उपयोग निम्न चीजों में देखते हैं-
खेतों, प्लॉट्स और क्षेत्रों को मापना
सिरेमिक टाइल की माप
छत का झुकाव; इमारत की ऊंचाई, चौड़ाई और लंबाई के लिए त्रिकोणमिति की आवश्यकता होती है।
वास्तुकारों द्वारा संरचनात्मक भार, छत के ढलानों, जमीन की सतहों आदि में त्रिकोणमिति का उपयोग होता है।
त्रिकोणमिति रेश्यो किन्हें कहते हैं?
किसी समकोण त्रिभुज में किन्हीं दो भुजाओं के अनुपात को त्रिकोणमितीय अनुपात या त्रिकोणमितीय रेश्यो कहते हैं। Trigonometry in Hindi में भुजाओं के नाम लंब (perpendicular), कर्ण (Hypotenuse) औऱ आधार (base) हैं। नीचे त्रिकोणमिति रेश्यो के बारे में बताया गया है-
sin θ = लंब/कर्ण
cos θ = आधार/कर्ण
tan θ = लम्ब/आधार
cosec θ = कर्ण/लंब
sec θ = कर्ण/आधार
cot θ = आधार/लंब।
पाइथागोरस प्रमेय का सूत्र क्या है?
पाइथागोरस प्रमेय का सूत्र कर्ण2 = आधार2 + लंब2
त्रिकोणमिति की टेबल?
ज्यामिति के साथ आपको 0°, 30°, 45°, 60° और 90° के विभिन्न त्रिकोणमितीय कोणों के निर्माण के बारे में पता होना चाहिए। त्रिकोणमिति को कोणो को परिभाषित करते हुए टेबल नीचे दी गई है-
| θ | 0° | 30° | 45° | 60° | 90° |
| sin | 0 | 1/2 | 1/2 | 3/2 | 1 |
| cos | 1 | 3/2 | 1/2 | 1/2 | 0 |
| ten | 0 | 1/3 | 1 | 3 | ∞ |
| cosec | ∞ | 3 | 1 | 1/3 | 0 |
| sec | 1 | 2/3 | 2 | 2 | ∞ |
| cot | ∞ | 2 | 2 | 2/3 | 1 |
